【迁移】时空图：以天狼星单程旅行为例

最近看《从一到无穷大》，对里面的闵氏时空图很感兴趣，恰好里面有去天狼星的例子，因此想用时空图画画看。为简化问题，这里取天狼星到地球的距离为 9 光年，实际约为 8.6 光年。同时为了便于画图，纵轴时间轴以年 × 光速为单位，横轴空间轴以光年为单位。使用 geogebra 进行绘图。（此文为迁移到 xlog 的旧博文）

出发前的时空图#

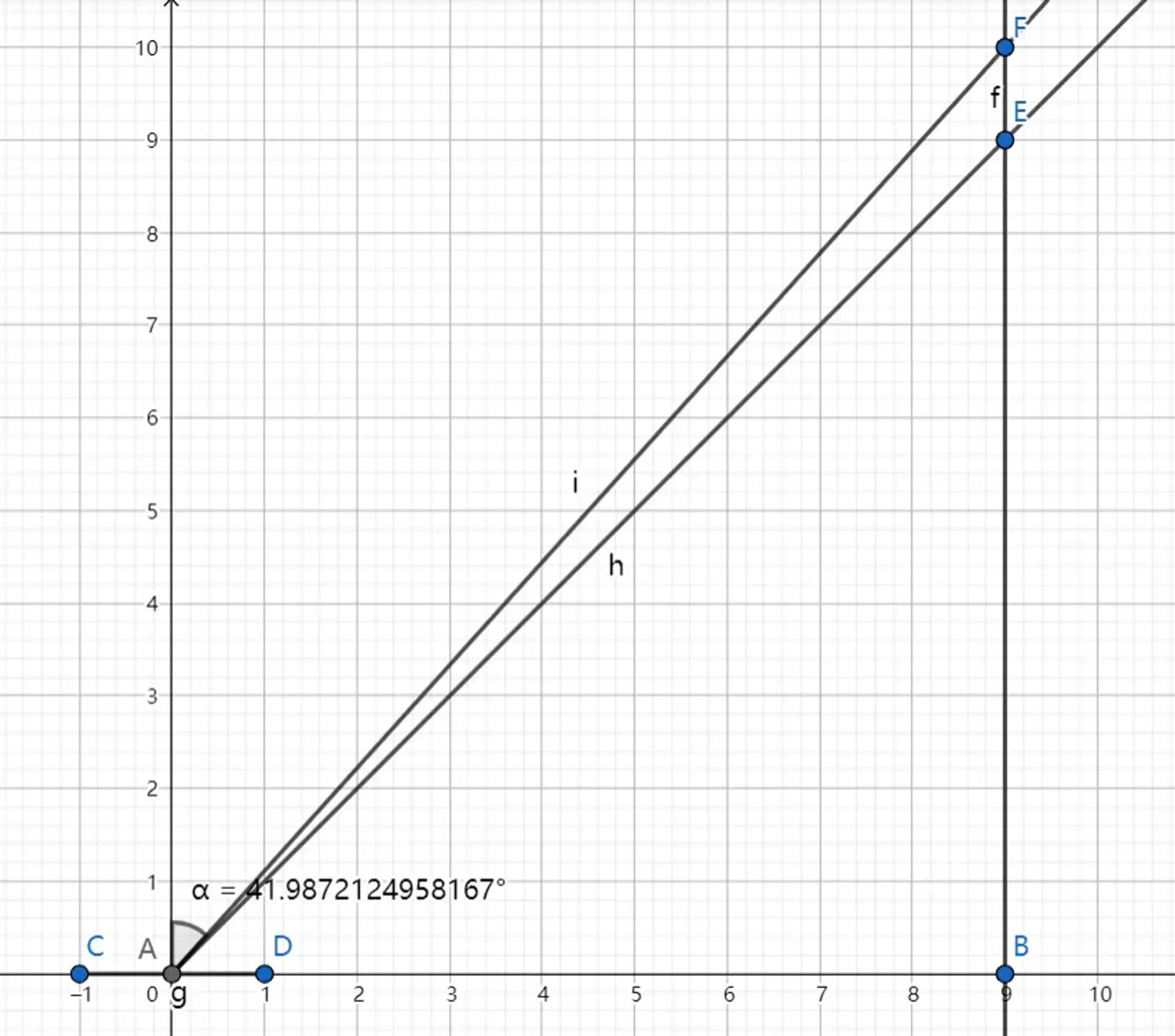
如图所示，线段 g（CAD）表示飞船，A 点为质心。直线 f 表示天狼星 B 的世界线。射线 h（AE）表示 A 的光锥。射线 i（AF）表示飞船的将来的世界线，其速度为 tanα=0.9 倍光速。

出发后的时空图#

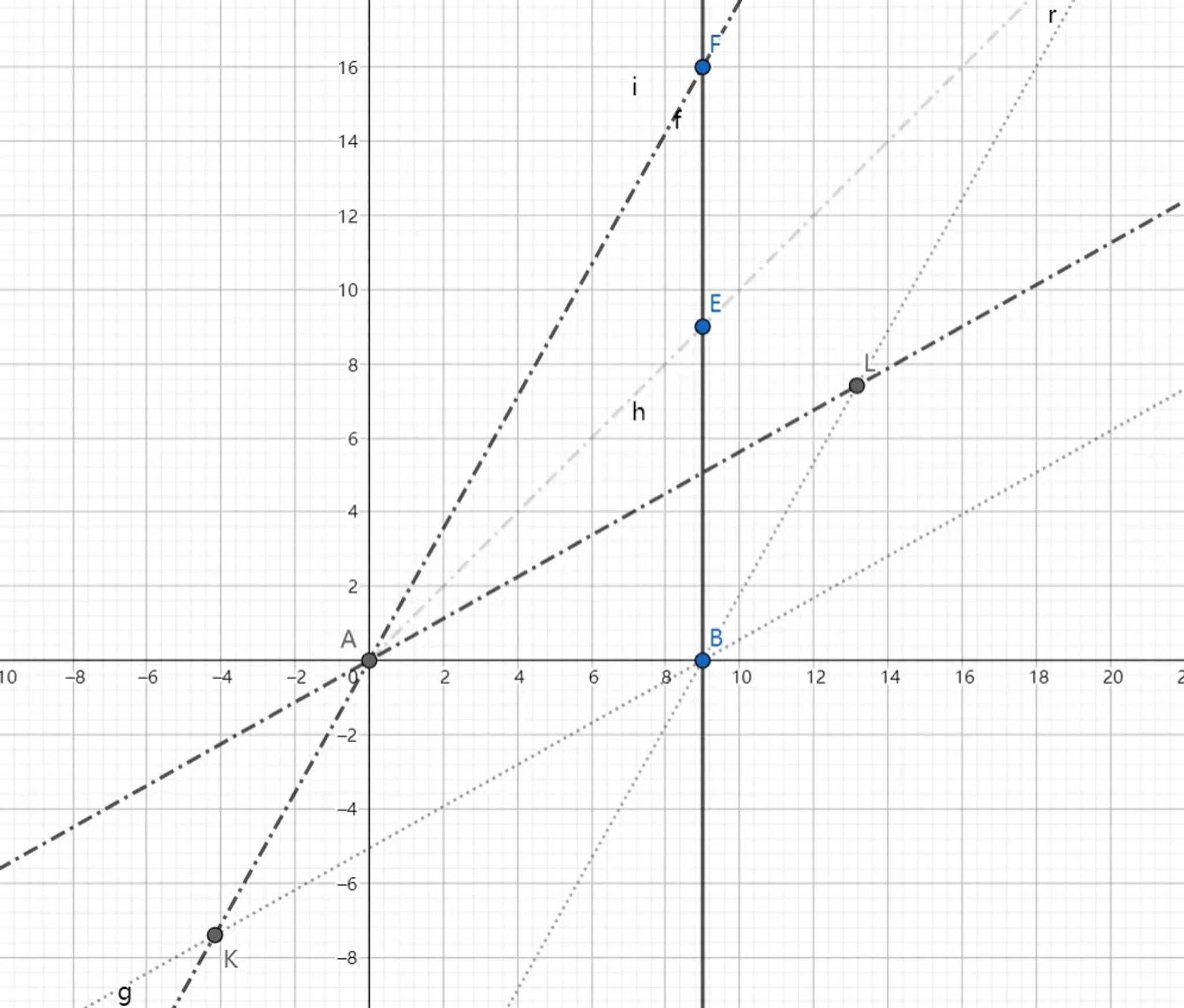
如图所示，为了便于绘图，减小了 α。直线 AF 与直线 AL 构成了以飞船为参考系的新时空坐标系。

x' 为 0 的直线 AF 为新的纵轴，t' 为 0 的直线 AL 为新的横轴，两者关于 AE 轴对称
AB 在新坐标系的几何位置为（AL，AK），物理位置为（ALβ，AKβ）

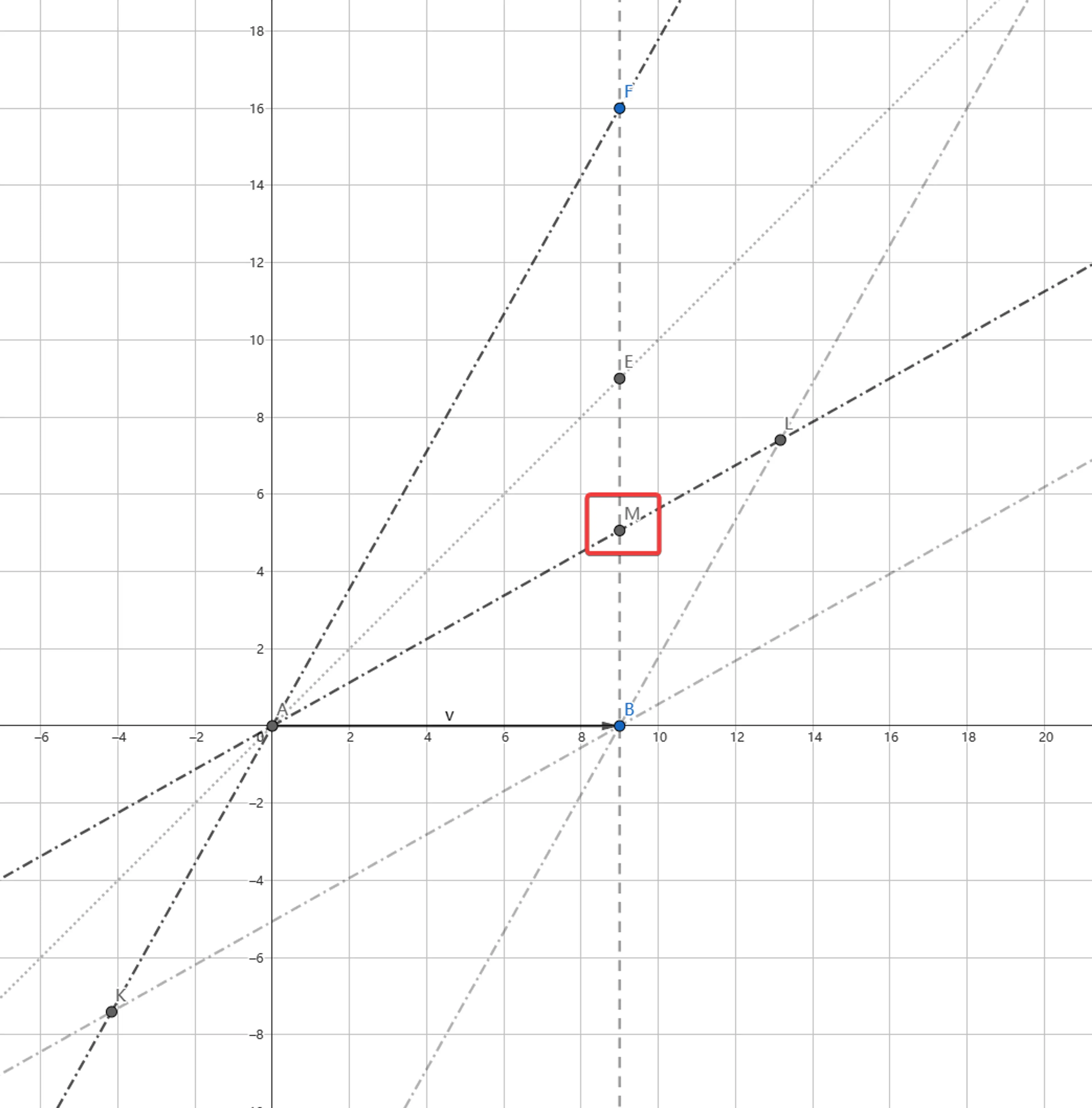
一些有趣的发现#

AB 的时空距离原来为 9，现在 AB' 的时空距离依然为 9，即 $9^2 + (0i)^2 = 20.65^2 + (-18.58i)^2$
AF、AL 上的单位对应的几何长度均变为原来的 1/β，即 $\lvert\overrightarrow{AF}\rvert\beta = t'_{ \overrightarrow{AF'}} \quad \lvert\overrightarrow{AL}\rvert\beta = x'_{ \overrightarrow{AB'}}$
对于出发的飞船上的人来说，旅行只花了 4.36 年，小于 10 年，即 $t'_{ \overrightarrow{AF'}} = 4.36 \lt 10 = t_{ \overrightarrow{AF}}$
对于出发的飞船上的人来说，天狼星距离为 3.92 光年，小于 9 光年，B' 点的天狼星是 18.58 年前的幻影，现在的天狼星是 M' 点的天狼星，即 $x'_{ \overrightarrow{AM'}} =(\frac{ \lvert\overrightarrow{AB}\rvert}{cos\alpha})\beta = 3.92 \lt 9 = x_{ \overrightarrow{AB}}$
对于出发的飞船上的人来说，天狼星靠近的速度 v = 3.92/4.36 = 0.9 倍光速，与外界观察飞船飞行的速度一致
飞船感知外界的空间长度 $x_{\overrightarrow{AB}} = 9$ 变成了空间长度 $x'_{\overrightarrow{AB'}} = \lvert\overrightarrow{AL}\rvert\beta = 20.65$ ，变长了 γ 倍，外界尺子变长了
飞船感知外界的时间长度 $t_{\overrightarrow{AF}} = 10$ 变成了时间长度 $t'_{ \overrightarrow{AF'}} = \lvert\overrightarrow{AF}\rvert\beta = 4.36$ ，缩短为 1/γ，外界时间变快了
飞船认为外界 “尺长钟快”，因此外界认为飞船上 “尺缩钟慢”
根据四维时空距离不变性，可以轻松计算飞船感知的旅程时间耗费，飞船参考系下的 AF' 的时空长度与外界参考系下 AF 的时空长度一致，即 $(i\lvert\overrightarrow{AF'}\rvert)^2 = (i\lvert\overrightarrow{AF}\rvert\beta)^2=AB^2+(iBF)^2$