【遷移】時空圖：以天狼星單程旅行為例

最近看《從一到無窮大》，對裡面的閔氏時空圖很感興趣，恰好裡面有去天狼星的例子，因此想用時空圖畫畫看。為簡化問題，這裡取天狼星到地球的距離為 9 光年，實際約為 8.6 光年。同時為了便於畫圖，縱軸時間軸以年 × 光速為單位，橫軸空間軸以光年為單位。使用 geogebra 進行繪圖。（此文為遷移到 xlog 的舊博文）

出發前的時空圖#

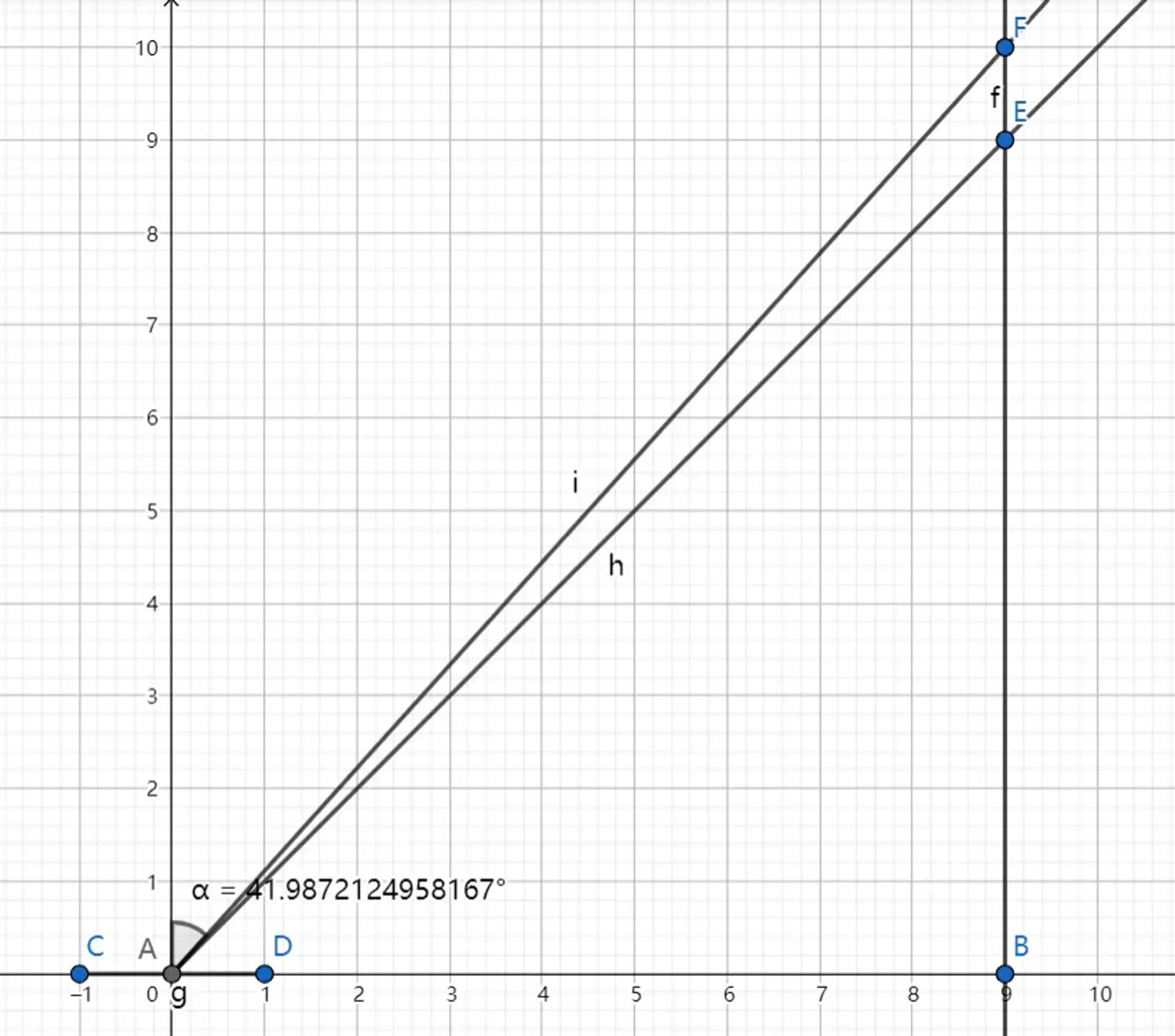
如圖所示，線段 g（CAD）表示飛船，A 點為質心。直線 f 表示天狼星 B 的世界線。射線 h（AE）表示 A 的光錐。射線 i（AF）表示飛船的將來的世界線，其速度為 tanα=0.9 倍光速。

出發後的時空圖#

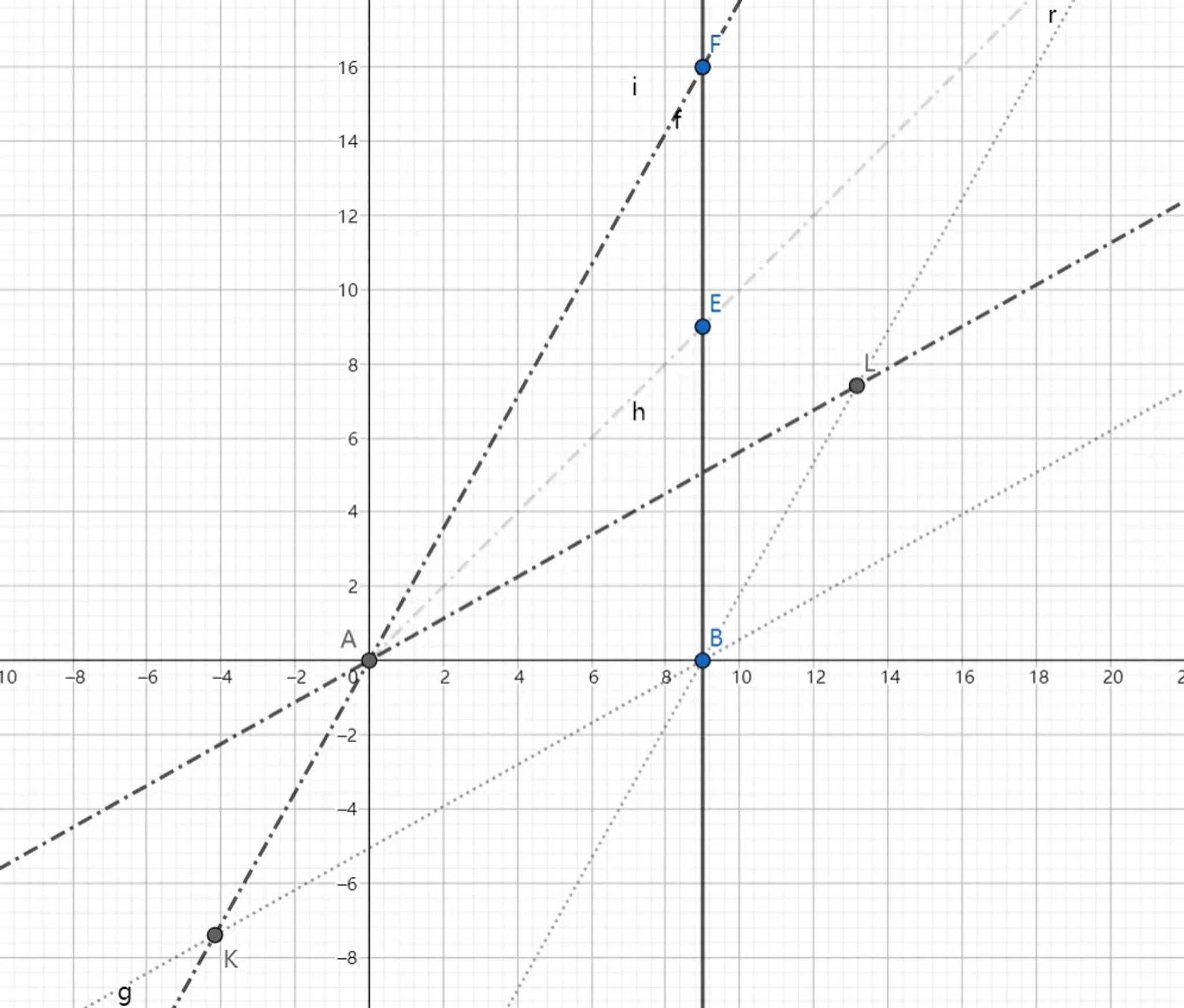
如圖所示，為了便於繪圖，減小了 α。直線 AF 與直線 AL 構成了以飛船為參考系的新時空座標系。

x' 為 0 的直線 AF 為新的縱軸，t' 為 0 的直線 AL 為新的橫軸，兩者關於 AE 軸對稱
AB 在新座標系的幾何位置為（AL，AK），物理位置為（ALβ，AKβ）

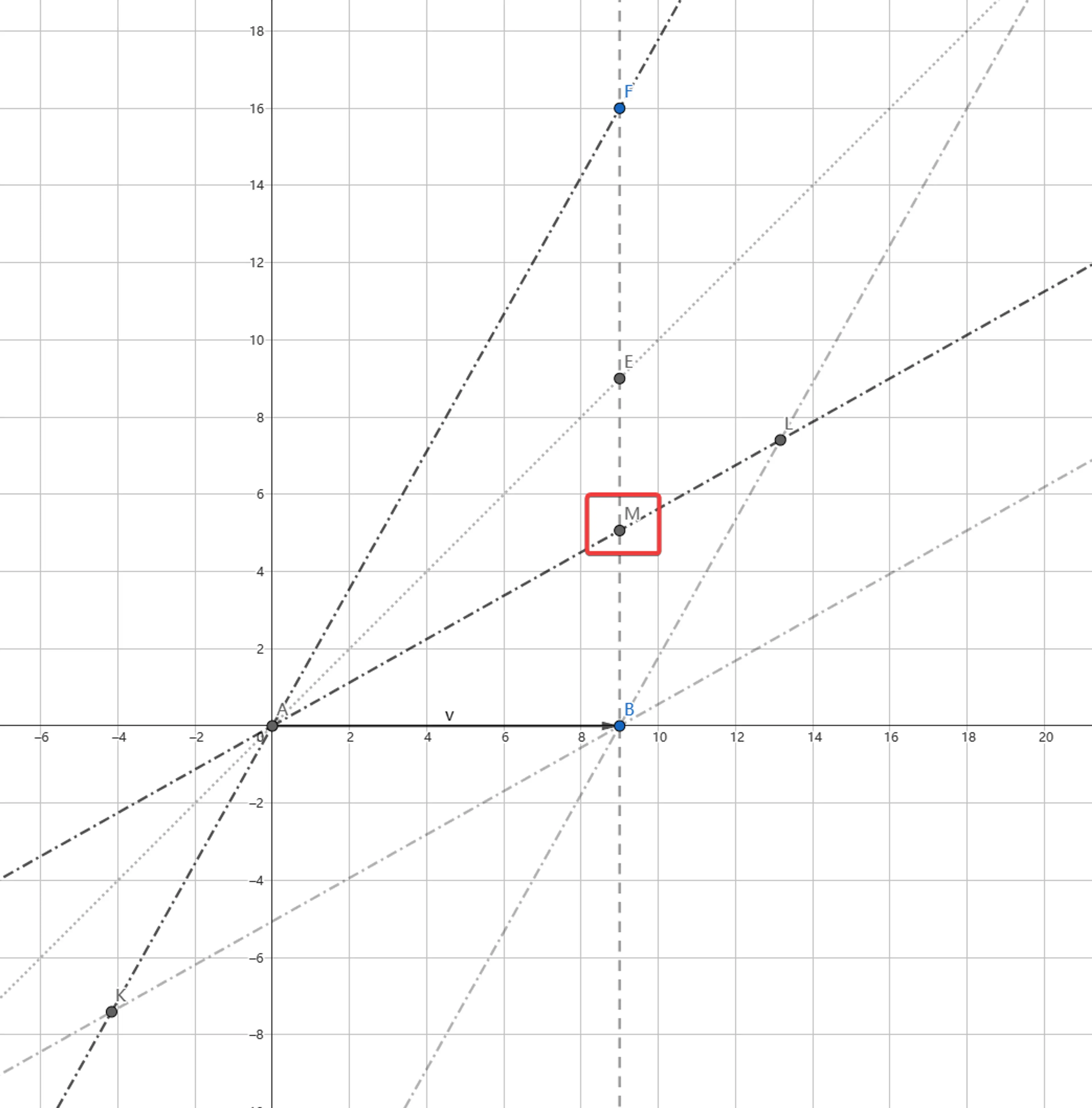
一些有趣的發現#

AB 的時空距離原來為 9，現在 AB' 的時空距離依然為 9，即 $9^2 + (0i)^2 = 20.65^2 + (-18.58i)^2$
AF、AL 上的單位對應的幾何長度均變為原來的 1/β，即 $\lvert\overrightarrow{AF}\rvert\beta = t'_{ \overrightarrow{AF'}} \quad \lvert\overrightarrow{AL}\rvert\beta = x'_{ \overrightarrow{AB'}}$
對於出發的飛船上的人來說，旅行只花了 4.36 年，小於 10 年，即 $t'_{ \overrightarrow{AF'}} = 4.36 \lt 10 = t_{ \overrightarrow{AF}}$
對於出發的飛船上的人來說，天狼星距離為 3.92 光年，小於 9 光年，B' 點的天狼星是 18.58 年前的幻影，現在的天狼星是 M' 點的天狼星，即 $x'_{ \overrightarrow{AM'}} =(\frac{ \lvert\overrightarrow{AB}\rvert}{cos\alpha})\beta = 3.92 \lt 9 = x_{ \overrightarrow{AB}}$
對於出發的飛船上的人來說，天狼星靠近的速度 v = 3.92/4.36 = 0.9 倍光速，與外界觀察飛船飛行的速度一致
飛船感知外界的空間長度 $x_{\overrightarrow{AB}} = 9$ 變成了空間長度 $x'_{\overrightarrow{AB'}} = \lvert\overrightarrow{AL}\rvert\beta = 20.65$ ，變長了 γ 倍，外界尺子變長了
飛船感知外界的時間長度 $t_{\overrightarrow{AF}} = 10$ 變成了時間長度 $t'_{ \overrightarrow{AF'}} = \lvert\overrightarrow{AF}\rvert\beta = 4.36$ ，縮短為 1/γ，外界時間變快了
飛船認為外界 “尺長鐘快”，因此外界認為飛船上 “尺縮鐘慢”
根據四維時空距離不變性，可以輕鬆計算飛船感知的旅程時間耗費，飛船參考系下的 AF' 的時空長度與外界參考系下 AF 的時空長度一致，即 $(i\lvert\overrightarrow{AF'}\rvert)^2 = (i\lvert\overrightarrow{AF}\rvert\beta)^2=AB^2+(iBF)^2$